LLMをコーディング
この記事では、ゼロからGPTライクなトランスフォーマーを実装します。 私の 前の記事で説明されている手順に従って、各セクションをコーディングします。
では、始めましょう。
環境準備
依存関係をインストールします。
pip install numpy requests torch tiktoken matplotlib pandas
import os
import requests
import pandas as pd
import matplotlib.pyplot as plt
import math
import tiktoken
import torch
import torch.nn as nn
Hyperparametersの設定
Hyperparametersは、訓練中にデータから学ぶことができないモデルの外部設定です。
これらは訓練プロセスが始まる前に設定され、訓練アルゴリズムの振る舞いと訓練されたモデルの性能を制御する上で重要な役割を果たします。
# Hyperparameters
batch_size = 4 # How many batches per training step
context_length = 16 # Length of the token chunk each batch
d_model = 64 # The vector size of the token embeddings
num_layers = 8 # Number of transformer blocks
num_heads = 4 # Number of heads in Multi-head attention # 我们的代码中通过 d_model / num_heads = 来获取 head_size
learning_rate = 1e-3 # 0.001
dropout = 0.1 # Dropout rate
max_iters = 5000 # Total of training iterations
eval_interval = 50 # How often to evaluate the model
eval_iters = 20 # How many iterations to average the loss over when evaluating the model
device = 'cuda' if torch.cuda.is_available() else 'cpu' # Instead of using the cpu, we'll use the GPU if it's available.
TORCH_SEED = 1337
torch.manual_seed(TORCH_SEED)
Datasetの準備
例にあるように、トレーニングには小規模なデータセットを使用します。
このデータセットは、セールスに関する教科書の内容が含まれているテキストファイルです。
このテキストファイルを使用して、セールステキストを生成できる言語モデルをトレーニングします。
# download a sample txt file from https://huggingface.co/datasets/goendalf666/sales-textbook_for_convincing_and_selling/raw/main/sales_textbook.txt
if not os.path.exists('sales_textbook.txt'):
url = 'https://huggingface.co/datasets/goendalf666/sales-textbook_for_convincing_and_selling/raw/main/sales_textbook.txt'
with open('sales_textbook.txt', 'w') as f:
f.write(requests.get(url).text)
with open('sales_textbook.txt', 'r', encoding='utf-8') as f:
text = f.read()
Step 1: トーク化
データセットをトークン化 tiktoken ライブラリを使用します。
このライブラリは高速で軽量なトークナイザーで、テキストをトークンにトークン化するために使用できます。
# Using TikToken to tokenize the source text
encoding = tiktoken.get_encoding("cl100k_base")
tokenized_text = encoding.encode(text) # size of tokenized source text is 77,919
vocab_size = len(set(tokenized_text)) # size of vocabulary is 3,771
max_token_value = max(tokenized_text)
print(f"Tokenized text size: {len(tokenized_text)}")
print(f"Vocabulary size: {vocab_size}")
print(f"The maximum value in the tokenized text is: {max_token_value}")
プリントされた出力:
Tokenized text size: 77919
Vocabulary size: 3771
The maximum value in the tokenized text is: 100069
Step 2: 単語の埋め込み
データセットをトレーニングセットとバリデーションセットに分割します。
トレーニングセットはモデルのトレーニングに使用され、バリデーションセットはモデルの性能を評価するために使用されます。
# Split train and validation
split_idx = int(len(tokenized_text) * 0.8)
train_data = tokenized_text[:split_idx]
val_data = tokenized_text[split_idx:]
# Prepare data for training batch
# Prepare data for training batch
data = train_data
idxs = torch.randint(low=0, high=len(data) - context_length, size=(batch_size,))
x_batch = torch.stack([data[idx:idx + context_length] for idx in idxs])
y_batch = torch.stack([data[idx + 1:idx + context_length + 1] for idx in idxs])
print(x_batch.shape, x_batch.shape)
プリントされた出力 (レーニング入力 x と y の形状):
torch.Size([4, 16]) torch.Size([4, 16])
Step 3: 位置エンコーディング
入力トークンをベクトルに変換するために、シンプルな埋め込みレイヤーを使用します。
# Define Token Embedding look-up table
token_embedding_lookup_table = nn.Embedding(max_token_value, d_model)
# Get X and Y embedding
x = token_embedding_lookup_table(x_batch.data)
y = token_embedding_lookup_table(y_batch.data)
現在、入力 x と y の両方とも形状(batch_size, context_length, d_model)になっています。
# Get x and y embedding
x = token_embedding_lookup_table(x_batch.data) # [4, 16, 64] [batch_size, context_length, d_model]
y = token_embedding_lookup_table(y_batch.data)
位置エンベディングの適用
元の論文で説明されているように、位置エンベディングテーブルを生成するためにサインとコサインを使用し、 これらの位置情報を入力埋め込みトークンに加えます。
# Define Position Encoding look-up table
position_encoding_lookup_table = torch.zeros(context_length, d_model) # initial with zeros with shape (context_length, d_model)
position = torch.arange(0, context_length, dtype=torch.float).unsqueeze(1)
# apply the sine & cosine
div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))
position_encoding_lookup_table[:, 0::2] = torch.sin(position * div_term)
position_encoding_lookup_table[:, 1::2] = torch.cos(position * div_term)
position_encoding_lookup_table = position_encoding_lookup_table.unsqueeze(0).expand(batch_size, -1, -1) #add batch to the first dimension
print("Position Encoding Look-up Table: ", position_encoding_lookup_table.shape)
プリントされた出力：
Position Encoding Look-up Table: torch.Size([4, 16, 64])
その後、入力埋め込みベクトルに位置エンコーディングを加えます。
# Add positional encoding into the input embedding vector
input_embedding_x = x + position_encoding_lookup_table # [4, 16, 64] [batch_size, context_length, d_model]
input_embedding_y = y + position_encoding_lookup_table
X = input_embedding_x
x_plot = input_embedding_x[0].detach().cpu().numpy()
print("Final Input Embedding of x: \n", pd.DataFrame(x_plot))
これで、トランスフォーマーブロックに供給される値である final input embedding of X を取得しました。
Final Input Embedding of x:
0 1 2 3 4 5 6 7 8 9 ... 54 55 56 57 58 59 60 61 62 63
0 -1.782388 1.200549 -0.177262 0.278616 -1.322919 0.929397 -0.178307 1.453488 -0.216367 -2.049190 ... -0.009743 2.694576 -0.592321 1.235002 1.137691 1.076938 -1.583359 1.994682 -0.411284 2.365598
1 0.434183 2.051380 0.642167 1.294858 0.287493 -0.132648 -0.388530 0.106470 0.515283 1.686583 ... 0.423079 0.564006 -1.514647 0.263115 -2.233931 1.759137 2.413690 -0.372896 0.512504 2.831246
2 0.180579 -0.714483 0.983105 -0.944209 1.182870 -0.100558 0.807144 0.232830 -0.455422 2.246022 ... 0.056277 0.913973 -0.200273 0.688581 1.302482 2.202587 -0.980815 -0.181238 0.747766 1.742957
3 -0.249654 -3.228277 -0.017824 0.492374 0.992460 -1.281102 0.811163 0.678884 0.251492 0.319295 ... 1.329760 1.259970 -0.345209 1.030813 0.629613 1.289158 0.586766 0.970829 1.487210 0.858970
4 1.533710 -1.794257 -0.115366 -2.216147 0.143978 -2.549789 0.285271 0.908505 -1.371307 1.000596 ... -0.171948 1.476006 -0.411271 2.187133 0.580001 1.330921 -0.996333 3.353865 0.216231 -0.570538
5 -2.187219 -0.290028 -0.914946 -0.614617 -0.033163 -1.060609 2.265111 -1.180711 1.237476 0.817889 ... 1.869089 0.720627 -1.679796 1.405375 0.399367 0.725817 -0.047124 -0.977291 0.013971 0.819522
6 -1.015749 1.862600 0.785039 2.425240 0.613279 -1.725359 1.288837 -1.810941 2.514978 0.433844 ... 0.408046 1.537934 -0.192739 0.709489 0.535088 -0.347714 -2.239857 -0.033674 0.192698 -0.136556
7 -0.446721 1.136845 0.336349 1.287424 1.515973 0.814479 0.233362 -1.706994 -0.438097 -0.674278 ... 0.697751 0.913269 -0.332155 -0.149376 0.140298 2.597988 0.219866 1.489297 1.089043 -1.265491
8 -0.190227 -0.968500 -1.648937 2.915030 -3.227971 -0.739308 -0.485671 -0.869817 -0.153695 -1.206717 ... 1.403767 0.636459 0.094945 -0.747135 0.495720 0.164661 -0.610816 0.730676 0.587971 2.341617
9 -0.224795 -0.326915 -0.362390 1.489488 -0.389251 -0.362224 0.913598 -2.051510 0.778566 -0.696349 ... 0.394737 1.314234 -0.124517 1.888481 0.689187 0.396996 1.056659 0.785319 1.079981 -0.194575
10 -0.692015 -1.732475 2.214933 -1.991298 -0.398353 1.266861 -1.057534 -1.157881 -0.801310 -0.614316 ... -1.901223 -0.854748 0.163998 0.173750 -1.058628 1.532371 -0.257311 1.359694 1.033851 0.677123
11 0.713966 -0.232073 2.291222 0.224710 -1.199412 0.022869 -1.532023 -0.403545 -0.262371 -1.097961 ... 1.827974 0.126189 1.134699 0.425639 -1.347956 0.086310 -0.774953 1.218501 -1.761807 0.117464
12 -0.468460 1.830461 1.335220 -1.410995 0.069466 1.672440 -1.680814 -1.598549 0.521277 -1.871883 ... -1.775825 -0.046493 0.723062 1.785805 1.166462 2.608919 1.078712 2.193650 1.377550 1.002753
13 1.436239 0.494849 1.781795 0.060173 0.538164 1.890070 -2.363284 2.231389 -1.082167 0.040986 ... -0.764243 -1.155260 0.084449 1.592648 0.105955 1.080390 -1.063937 0.691866 -0.906071 0.383779
14 -0.113100 0.519679 0.316672 0.299135 3.229518 1.496113 -0.325615 0.203938 -2.198124 -0.356190 ... 0.700703 0.913256 -0.329941 -0.149384 0.141958 2.597984 0.221110 1.489295 1.089976 -1.265493
15 0.301521 0.997564 -0.672755 -1.215677 0.949777 0.474997 -0.279164 1.144048 -1.059472 0.068650 ... 0.796498 -1.032138 0.977697 0.790623 0.725540 1.646803 1.253047 0.296801 0.798098 2.022164
[16 rows x 64 columns]
注：yの埋め込みベクトルはxと同じ形状になります。
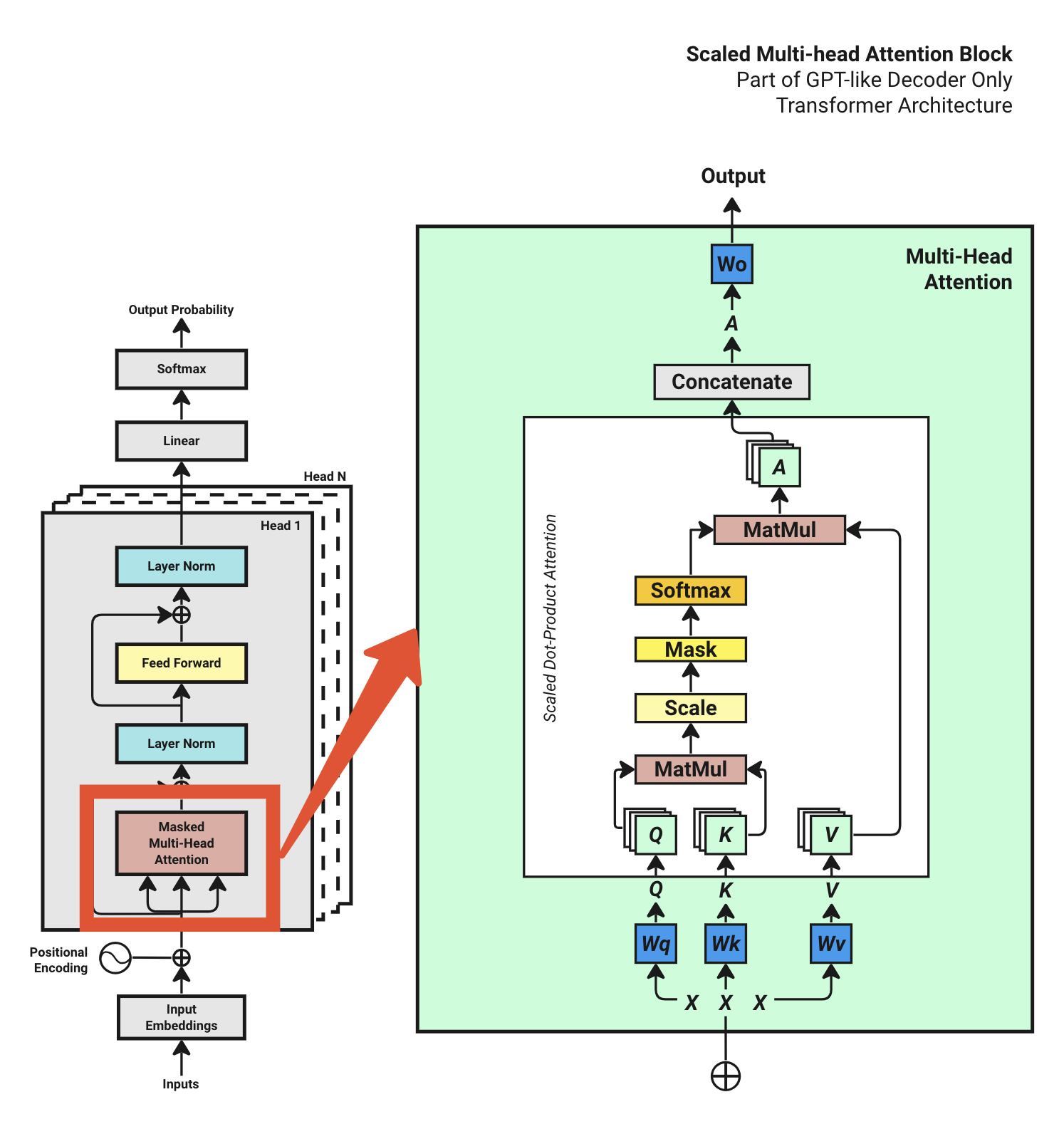
Step 4: トランスフォーマーブロック
4.1 マルチヘッドアテンションの概要
マルチヘッドアテンションの図を再度見てみましょう。
入力埋め込み X を取得したので、マルチヘッドアテンションブロックの実装を開始できます。
マルチヘッドアテンションブロックを実装するには、いくつかのステップがあります。一つずつコード化していきましょう。
4.2 Q,K,Vの準備
# Prepare Query, Key, Value for Multi-head Attention
query = key = value = X # [4, 16, 64] [batch_size, context_length, d_model]
# Define Query, Key, Value weight matrices
Wq = nn.Linear(d_model, d_model)
Wk = nn.Linear(d_model, d_model)
Wv = nn.Linear(d_model, d_model)
Q = Wq(query) #[4, 16, 64]
Q = Q.view(batch_size, -1, num_heads, d_model // num_heads) #[4, 16, 4, 16]
K = Wk(key) #[4, 16, 64]
K = K.view(batch_size, -1, num_heads, d_model // num_heads) #[4, 16, 4, 16]
V = Wv(value) #[4, 16, 64]
V = V.view(batch_size, -1, num_heads, d_model // num_heads) #[4, 16, 4, 16]
その後、 Q, K, V to [batch_size, num_heads, context_length, head_size] の形に再構成し、さらなる計算のために準備します。
# Transpose q,k,v from [batch_size, context_length, num_heads, head_size] to [batch_size, num_heads, context_length, head_size]
# The reason is that treat each batch with "num_heads" as its first dimension.
Q = Q.transpose(1, 2) # [4, 4, 16, 16]
K = K.transpose(1, 2) # [4, 4, 16, 16]
V = V.transpose(1, 2) # [4, 4, 16, 16]
4.3 QK^T アテンションの計算
これは torch.matmul 関数を使用することで非常に簡単に行えます。
# Calculate the attention score betwee Q and K^T
attention_score = torch.matmul(Q, K.transpose(-2, -1))
4.4 スケール
# Then Scale the attention score by the square root of the head size
attention_score = attention_score / math.sqrt(d_model // num_heads)
実際には、4.3 と 4.4 を一行で書き換えることができます。
attention_score = torch.matmul(Q, K.transpose(-2, -1)) / math.sqrt(d_model // num_heads) # [4, 4, 16, 16] #[4, 4, 16, 16] [batch_size, num_heads, context_length, context_length]
print(pd.DataFrame(attention_score[0][0].detach().cpu().numpy()))
プリントされた出力：
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
0 0.105279 -0.365092 -0.339839 -0.650558 -0.464043 -0.531401 0.437939 -0.650732 -0.616331 -0.429000 -0.332607 0.080401 0.000111 -0.601670 -0.783942 0.147967
1 -0.302636 0.525435 0.863502 -0.218539 0.600691 -0.413970 0.408111 0.765074 -0.376257 0.233526 0.915393 -0.263153 0.683832 0.430964 0.802033 0.281169
2 0.201820 0.156336 -0.245585 0.101653 0.228243 -0.565197 0.589193 -0.579525 -0.080071 0.078848 -0.471447 0.481268 -0.129725 -0.123364 -0.963065 -0.582126
3 0.517998 -0.303064 0.484515 -0.399551 -0.004528 -0.028223 -0.602194 0.107085 -0.504462 0.017590 0.592893 -0.750240 0.022489 -0.014217 -0.038678 0.484633
4 0.519200 0.322036 0.328027 -0.031755 0.006269 0.133609 -0.095071 -0.252013 0.096449 -0.268063 -0.306129 -0.045432 -0.027766 -0.163095 -0.338737 0.712901
5 -0.635913 0.137114 0.083046 0.234778 -0.668992 -0.366838 -0.613126 0.245075 -0.042131 0.221872 0.806992 -0.279996 0.046113 0.646270 0.284564 0.478298
6 -0.287777 -0.841604 -0.128455 -0.566180 0.079559 -0.530863 -0.082675 0.072495 -0.264806 -0.229649 0.269325 -0.185602 -0.366693 -0.321176 -0.130587 0.416121
7 -0.798519 -0.905525 0.317880 -0.176577 0.751465 -0.564863 1.014724 -0.068284 -0.527703 0.118972 0.085287 -0.102589 -0.640548 0.376717 -0.120097 0.164074
8 0.141614 -0.022169 0.152088 -0.519404 -0.069152 -0.880496 -0.229767 -0.849347 -0.539544 -0.510258 -0.246146 -0.266640 -0.086958 -0.577571 -1.191547 0.050306
9 -0.097493 0.860376 0.073501 0.150553 -0.651579 -0.376676 -0.691368 0.315606 0.135982 0.292198 0.774460 -0.131879 0.626085 0.452120 0.153703 0.082386
10 -0.469827 0.302545 -0.015767 -0.175387 -0.049927 -0.706852 0.511237 0.043908 -0.492887 -0.168435 -0.167744 0.016956 0.141400 -0.102674 -0.072396 -0.261558
11 -0.335474 -0.399539 -0.093901 -0.682290 0.312682 -0.310319 0.344753 0.017465 -0.364808 -0.262316 -0.282589 -0.239767 0.008904 -0.621042 -0.261246 -0.214888
12 -1.757631 -0.967825 -0.516159 -0.246766 -0.352132 -0.780370 -0.262975 -0.793605 -0.238561 -0.374695 -0.132526 -0.126956 -0.524015 -0.194315 -1.046538 -0.402560
13 0.550975 0.313643 -0.074468 0.519995 -0.149188 -0.565922 0.199527 -0.738029 0.142203 -0.164007 -0.494203 0.570010 -0.579608 -0.198923 -0.869503 -0.120218
14 -0.616347 -0.812240 0.245260 0.167278 0.913596 -0.493119 1.139083 -0.300623 -0.399155 0.200648 -0.114634 0.147219 -0.829207 0.363519 -0.325846 0.026840
15 -0.145391 0.514632 -0.296119 -0.038103 -0.187110 -0.634636 0.509902 -0.338267 -0.231534 -0.007304 -0.432799 0.339123 0.248173 -0.242426 -0.595925 -0.442379
4.5 マスク
# Apply Mask to attention scores
attention_score = attention_score.masked_fill(torch.triu(torch.ones(attention_score.shape[-2:]), diagonal=1).bool(), float('-inf')) #[4, 4, 16, 16] [batch_size, num_heads, context_length, context_length]
print(pd.DataFrame(attention_score[0][0].detach().cpu().numpy()))
プリントされた出力 (バッチその1のケース):
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
```text
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
0 0.105279 -inf -inf -inf -inf -inf -inf -inf -inf -inf -inf -inf -inf -inf -inf -inf
1 -0.302636 0.525435 -inf -inf -inf -inf -inf -inf -inf -inf -inf -inf -inf -inf -inf -inf
2 0.201820 0.156336 -0.245585 -inf -inf -inf -inf -inf -inf -inf -inf -inf -inf -inf -inf -inf
3 0.517998 -0.303064 0.484515 -0.399551 -inf -inf -inf -inf -inf -inf -inf -inf -inf -inf -inf -inf
4 0.519200 0.322036 0.328027 -0.031755 0.006269 -inf -inf -inf -inf -inf -inf -inf -inf -inf -inf -inf
5 -0.635913 0.137114 0.083046 0.234778 -0.668992 -0.366838 -inf -inf -inf -inf -inf -inf -inf -inf -inf -inf
6 -0.287777 -0.841604 -0.128455 -0.566180 0.079559 -0.530863 -0.082675 -inf -inf -inf -inf -inf -inf -inf -inf -inf
7 -0.798519 -0.905525 0.317880 -0.176577 0.751465 -0.564863 1.014724 -0.068284 -inf -inf -inf -inf -inf -inf -inf -inf
8 0.141614 -0.022169 0.152088 -0.519404 -0.069152 -0.880496 -0.229767 -0.849347 -0.539544 -inf -inf -inf -inf -inf -inf -inf
9 -0.097493 0.860376 0.073501 0.150553 -0.651579 -0.376676 -0.691368 0.315606 0.135982 0.292198 -inf -inf -inf -inf -inf -inf
10 -0.469827 0.302545 -0.015767 -0.175387 -0.049927 -0.706852 0.511237 0.043908 -0.492887 -0.168435 -0.167744 -inf -inf -inf -inf -inf
11 -0.335474 -0.399539 -0.093901 -0.682290 0.312682 -0.310319 0.344753 0.017465 -0.364808 -0.262316 -0.282589 -0.239767 -inf -inf -inf -inf
12 -1.757631 -0.967825 -0.516159 -0.246766 -0.352132 -0.780370 -0.262975 -0.793605 -0.238561 -0.374695 -0.132526 -0.126956 -0.524015 -inf -inf -inf
13 0.550975 0.313643 -0.074468 0.519995 -0.149188 -0.565922 0.199527 -0.738029 0.142203 -0.164007 -0.494203 0.570010 -0.579608 -0.198923 -inf -inf
14 -0.616347 -0.812240 0.245260 0.167278 0.913596 -0.493119 1.139083 -0.300623 -0.399155 0.200648 -0.114634 0.147219 -0.829207 0.363519 -0.325846 -inf
15 -0.145391 0.514632 -0.296119 -0.038103 -0.187110 -0.634636 0.509902 -0.338267 -0.231534 -0.007304 -0.432799 0.339123 0.248173 -0.242426 -0.595925 -0.442379
上記の通り、対角線と上三角形は-infでマスクされています。
4.6 ソフトマックス
# Softmax the attention score
attention_score = torch.softmax(attention_score, dim=-1) #[4, 4, 16, 16] [batch_size, num_heads, context_length, context_length]
print(pd.DataFrame(attention_score.detach().cpu().numpy()))
プリントされた出力 (バッチその1のケース):
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
0 0.062604 0.062472 0.062478 0.062419 0.062452 0.062439 0.062748 0.062419 0.062424 0.062459 0.062479 0.062595 0.062568 0.062427 0.062399 0.062619
1 0.062377 0.062529 0.062643 0.062387 0.062551 0.062364 0.062499 0.062605 0.062368 0.062460 0.062664 0.062381 0.062577 0.062505 0.062619 0.062470
2 0.062565 0.062551 0.062453 0.062535 0.062574 0.062400 0.062717 0.062398 0.062488 0.062529 0.062414 0.062668 0.062477 0.062479 0.062354 0.062398
3 0.062647 0.062427 0.062634 0.062411 0.062486 0.062480 0.062384 0.062513 0.062396 0.062491 0.062679 0.062367 0.062492 0.062483 0.062478 0.062634
4 0.062635 0.062566 0.062567 0.062473 0.062481 0.062512 0.062460 0.062430 0.062502 0.062428 0.062421 0.062470 0.062474 0.062446 0.062416 0.062720
5 0.062371 0.062501 0.062488 0.062527 0.062367 0.062405 0.062373 0.062529 0.062461 0.062523 0.062744 0.062418 0.062480 0.062669 0.062541 0.062603
6 0.062467 0.062379 0.062504 0.062417 0.062562 0.062422 0.062516 0.062560 0.062472 0.062480 0.062628 0.062490 0.062451 0.062460 0.062503 0.062689
7 0.062358 0.062348 0.062566 0.062444 0.062742 0.062384 0.062900 0.062465 0.062389 0.062509 0.062500 0.062458 0.062375 0.062585 0.062455 0.062521
8 0.062632 0.062573 0.062636 0.062449 0.062559 0.062391 0.062513 0.062395 0.062445 0.062450 0.062509 0.062504 0.062553 0.062438 0.062356 0.062598
9 0.062434 0.062727 0.062467 0.062484 0.062360 0.062391 0.062356 0.062525 0.062480 0.062519 0.062687 0.062428 0.062625 0.062565 0.062484 0.062469
10 0.062419 0.062608 0.062511 0.062473 0.062502 0.062385 0.062693 0.062527 0.062415 0.062475 0.062475 0.062520 0.062555 0.062490 0.062497 0.062455
11 0.062463 0.062450 0.062519 0.062403 0.062655 0.062468 0.062669 0.062551 0.062457 0.062478 0.062474 0.062484 0.062548 0.062412 0.062479 0.062489
12 0.062327 0.062405 0.062489 0.062561 0.062530 0.062435 0.062556 0.062433 0.062564 0.062524 0.062599 0.062601 0.062487 0.062578 0.062394 0.062517
13 0.062685 0.062591 0.062482 0.062671 0.062466 0.062395 0.062554 0.062374 0.062538 0.062463 0.062405 0.062693 0.062393 0.062456 0.062360 0.062472
14 0.062372 0.062352 0.062530 0.062509 0.062806 0.062387 0.062958 0.062414 0.062400 0.062518 0.062447 0.062504 0.062350 0.062566 0.062410 0.062476
15 0.062479 0.062693 0.062448 0.062504 0.062470 0.062394 0.062691 0.062440 0.062460 0.062512 0.062424 0.062620 0.062588 0.062458 0.062399 0.062422
ソフトマックス関数を適用した後、スコアは0から1の間になり、各行の合計は1になります。
4.7 V アテンションの計算
最後に、アテンションスコアに V を掛けて、マルチヘッドアテンションブロックの出力を得ます。
# Calculate the V attention output
A = torch.matmul(attention_score, V) # [4, 4, 16, 16] [batch_size, num_heads, context_length, head_size]
print(attention_output.shape)
プリントされた出力：
torch.Size([4, 4, 16, 16])
注: 現在の形状は [4, 4, 16, 16] すなわち [batch_size, num_heads, context_length, head_size] です。
4.8 結合と出力
前回の記事 で述べたように、マルチヘッドアテンションブロックの出力を結合して線形レイヤーに供給する必要があります。
A = A.transpose(1, 2) # [4, 16, 4, 16] [batch_size, context_length, num_heads, head_size]
A = A.reshape(batch_size, -1, d_model) # [4, 16, 64] [batch_size, context_length, d_model]
_注: 現在の形状は [4, 16, 64] すなわち [batch_size, context_length, d_model] です。
これで [64,64] の線形レイヤー Wo (トレーニング中に学習される重み) を適用し、 マルチヘッドアテンションブロックの最終出力を得ることができます：
# Define the output weight matrix
Wo = nn.Linear(d_model, d_model)
output = Wo(A) # [4, 16, 64] [batch_size, context_length, d_model]
print(output.shape)
出力をプリントすると、形状は元の入力埋め込みの形状である [4, 16, 64] に戻ります。
Step 5: 残差接続とレイヤー正規化
マルチヘッドアテンションブロックの出力が得られたので、残差接続とレイヤー正規化を適用できます。
# Add residual connection
output = output + X
# Add Layer Normalization
layer_norm = nn.LayerNorm(d_model)
output = layer_norm(output)
Step 6: フィードフォワードネットワーク
# Define Feed Forward Network
output = nn.Linear(d_model, d_model * 4)(output)
output = nn.ReLU()(output)
output = nn.Linear(d_model * 4, d_model)(output)
output = torch.dropout(output, p=dropout, train=True)
最後の残差接続とレイヤー正規化を追加します：
# Add residual connection
output = output + X
# Add Layer Normalization
layer_norm = nn.LayerNorm(d_model)
output = layer_norm(output)
Step 7: ステップ4から6を繰り返す
上記で完了したのは、たった一つのトランスフォーマーブロックです。 実際には、複数のトランスフォーマーブロックを積み重ねて、トランスフォーマーデコーダを形成します。
実際には、コードをクラスにパッケージ化し、PyTorchのnn.Moduleを使用してトランスフォーマーデコーダを構築するべきです。 しかし、デモンストレーションのため、一つのブロックのままにしておきます。
Step 8: 出力確率
最終的な線形レイヤーを適用して、ロジットを取得します：
logits = nn.Linear(d_model, max_token_value)(output)
print(pd.DataFrame(logits[0].detach().cpu().numpy()))
最後のステップは、各トークンの確率を得るために、ロジットに ソフトマックス を適用することです：
# torch.softmax usually used during inference, during training we use torch.nn.CrossEntropyLoss
# but for illustration purpose, we'll use torch.softmax here
probabilities = torch.softmax(logits, dim=-1)
0 1 2 3 4 5 6 7 8 9 ... 100059 100060 100061 100062 100063 100064 100065 100066 100067 100068
0 0.000007 0.000008 0.000006 0.000005 0.000004 0.000004 0.000009 0.000007 0.000009 0.000008 ... 0.000013 0.000005 0.000006 0.000014 0.000009 0.000005 0.000005 0.000016 0.000006 0.000005
1 0.000018 0.000016 0.000006 0.000017 0.000005 0.000006 0.000005 0.000005 0.000008 0.000004 ... 0.000006 0.000004 0.000006 0.000007 0.000006 0.000007 0.000014 0.000020 0.000004 0.000001
2 0.000013 0.000007 0.000008 0.000003 0.000007 0.000009 0.000021 0.000005 0.000007 0.000013 ... 0.000018 0.000009 0.000010 0.000010 0.000018 0.000009 0.000007 0.000008 0.000005 0.000015
3 0.000005 0.000013 0.000011 0.000004 0.000006 0.000007 0.000012 0.000006 0.000015 0.000010 ... 0.000032 0.000006 0.000008 0.000005 0.000014 0.000009 0.000021 0.000014 0.000004 0.000005
4 0.000005 0.000010 0.000008 0.000006 0.000017 0.000005 0.000010 0.000003 0.000008 0.000010 ... 0.000012 0.000005 0.000010 0.000003 0.000015 0.000022 0.000015 0.000010 0.000013 0.000005
5 0.000008 0.000004 0.000007 0.000003 0.000004 0.000011 0.000018 0.000007 0.000002 0.000010 ... 0.000013 0.000004 0.000012 0.000010 0.000015 0.000017 0.000010 0.000019 0.000013 0.000012
6 0.000005 0.000008 0.000014 0.000004 0.000007 0.000007 0.000012 0.000016 0.000005 0.000005 ... 0.000012 0.000007 0.000012 0.000022 0.000011 0.000018 0.000011 0.000010 0.000004 0.000014
7 0.000004 0.000008 0.000003 0.000006 0.000005 0.000019 0.000010 0.000016 0.000007 0.000011 ... 0.000014 0.000007 0.000007 0.000010 0.000013 0.000012 0.000013 0.000003 0.000008 0.000004
8 0.000002 0.000006 0.000005 0.000004 0.000006 0.000010 0.000008 0.000006 0.000016 0.000012 ... 0.000022 0.000004 0.000006 0.000011 0.000031 0.000016 0.000022 0.000006 0.000006 0.000005
9 0.000006 0.000005 0.000010 0.000008 0.000019 0.000018 0.000012 0.000011 0.000005 0.000015 ... 0.000019 0.000008 0.000005 0.000029 0.000009 0.000010 0.000009 0.000017 0.000007 0.000007
10 0.000011 0.000005 0.000008 0.000007 0.000017 0.000009 0.000007 0.000013 0.000010 0.000008 ... 0.000015 0.000011 0.000012 0.000007 0.000012 0.000020 0.000010 0.000006 0.000011 0.000009
11 0.000011 0.000006 0.000004 0.000005 0.000006 0.000012 0.000009 0.000007 0.000007 0.000004 ... 0.000042 0.000011 0.000010 0.000010 0.000021 0.000009 0.000004 0.000021 0.000008 0.000014
12 0.000005 0.000010 0.000007 0.000009 0.000007 0.000023 0.000011 0.000005 0.000006 0.000006 ... 0.000015 0.000006 0.000009 0.000003 0.000019 0.000010 0.000009 0.000056 0.000017 0.000004
13 0.000004 0.000016 0.000010 0.000010 0.000026 0.000008 0.000009 0.000002 0.000008 0.000007 ... 0.000014 0.000006 0.000010 0.000010 0.000007 0.000012 0.000008 0.000009 0.000016 0.000006
14 0.000003 0.000008 0.000019 0.000007 0.000014 0.000004 0.000009 0.000009 0.000005 0.000004 ... 0.000014 0.000010 0.000010 0.000003 0.000007 0.000013 0.000013 0.000005 0.000013 0.000002
15 0.000005 0.000010 0.000008 0.000005 0.000011 0.000010 0.000009 0.000005 0.000004 0.000005 ... 0.000009 0.000007 0.000012 0.000006 0.000013 0.000013 0.000008 0.000014 0.000005 0.000005
[16 rows x 100069 columns]
注：ここで得られるものは、全語彙における各トークンの確率を表す巨大な行列で、 形状は [16, 100069] です。
完全な動作コード
実際には、複数のトランスフォーマーブロックが積み重ねられ、一つのデコーディング処理を行います。
そしてトレーニング中、出力トークンは正解トークンと比較され、損失を計算します。そして、ハイパーパラメータで定義された max_iters 回の回数だけプロセスを繰り返します。
私の GitHub に、完全に動作するトランスフォーマーデコーダのコードがありますので、ご覧になってください。
Last modified: 22 February 2024